Here is a selection of my favorite and most polished projects/experiments since I started college, sorted by period of interest (Most recent first).

Worst sorting algorithm ever but it’s an eigenvalue flow
Given a time-valued matrix function A(t), its eigenvalues and eigenvectors evolve as.: $$ \dot{\lambda}_i = \langle \dot{A} n_i,n_i\rangle \\ \dot{n}_i = \sum \frac{1}{\lambda_i - \lambda_j} \langle \dot{A} n_i,n_j\rangle n_j $$
By setting A(t) = A_0 + t(B-A_0) we know that the eigenvalues of A(t) must interpolate between the ones of A_0 and B but by remaining sorted along the way since the repulsive potential 1/(\lambda_i - \lambda_j) must always be finite. Hence, starting from A_0 with random eigenvectors and eigenvalues 1,…,n allows one to track the sorting to the target values encoded as the eigenvalues of B. This algorithm has a complexity of at least O(n^3) for each timestep and is numerically unstable ^^. Sorting by eigenvalues flow had been found with a different approach with Brockett flow.
Lattice Boltzman Method (LBM)
Canonical solver of the LBM in D2Q9.
- Two Relaxation Time (TRT) method for the collision operator.
- Dirichlet boundary conditions: $$ f_i(x,t) = f_i^{eq}(\rho,\vec{0}) \text{, } x\in \partial \Omega. $$
Curl visualized in blue/red. Amazing resources: book blog.
Markov-Chain Diffusion-Limited-Aggregation (MCDLA)
A Markov Chain interpretation of the DLA process. The idea is to replace the individual brownian motion simulation with the computation of the probability: $$ x\in \partial X_n, f_n(x) = \mathbb{P}\left(B_{\tau_n} = x | \tau_n < \infty \right) $$ where tau is the stopping time of a Brownian motion, coming from infinity, touching X_n, the DLA at stage n. Such computation is performed on a discrete grid as the fixpoint of the markov chain transition matrix with uniform diffusion except around the boundary of the DLA where the particles are stuck. The next stage of the DLA is computed as:
$$ X_{n+1} = X_n \cup \bigcup_{i = 1}^{\lfloor\sqrt{n}\rfloor} Y_i, \text{ where } Y_i \sim f_n $$

Forest Fire simulation by coupled discrete stochastic processes
- Simple discrete model
- Geometric laws of growth.
- Some interesting properties, for instance fire can disappear completely from a tree and come back later due to spreading.
- very tunable and upgradable

Road Generation
- A* algorithm for the main track, with weights on the vertices and on the edges to avoid height difference
- then, to get closer to a clothoïd, since they have affine curvature, I minimize the second derivative of the curvature by minimizing:
$$
\mathcal{E}(\gamma) = \int_0^1 ||\gamma^{(4)}(t)||^2 dt
$$
with an implicit scheme, where the curve is re-parametrized by arc-length at each iteration to have :
$$||\ddot{\gamma}|| = \kappa$$.
“Estimation of the volume of Voronoi cells in high dimension and control variables in Monte Carlo rendering”
4th year research project supervised by David Coeurjolly and Vincent Nivoliers
- Exploration of stochastic techniques in estimating the volume and barycenters of Voronoi cells in high dimension
- Improvement of Monte Carlo integration by control variate techniques, new control variate proposed
- Caracterization and proofs of domination of the new control variate over the original control variate

Image Segmentation : Region Growing and Split and Merge Algorithms
- Region Growing : use of more various metric (Wasserstein distance between histograms, Mahalanobis distance, Lp norms) to compare regions
- Efficient Split and Merge implementation using a quadtree structure and binary encoding to compute neighborhoods
Edge Detection : Hough Transform and improvements
- Implementation of the Active Contour Method for image segmentation
- Implementation of the Hough Transform for line detection
- New line detection algorithm based on DBScan in pixel-gradient space



Stable Fluids implementation
Standard Stable Fluids implementation :
- Diffusion
- Semi-Lagrangian advection
- Projection method with prefactored sparse laplacian matrix for poisson problem
$$\Delta u = \nabla \cdot v$$

Cloth simulation : Mass Spring System & XPBD
- Implementation of Mass Spring System
- Implementation of XPBD
- Spatial Hashing for fast collision detection
Ambiant Occlusion & Diffusion Limited Aggregation
- Quasi Monte Carlo techniques for Ambiant Occlusion on heightfields
- Improvement of DLA algorithm by simulating brownian motion in a Walk-On-Sphere way and Octree for closest point search


Use of Normal information to improve differential operators on polygonal meshes
1 month research internship supervised by David Coeurjolly.
- Various Spline based approaches to provide better estimates of non-linear edges in order improve the convergence of discretizations of differential operators based on Fernando De Goes et al. (No conclusive results)

Curves & Clouds - A scientific visualization and computing library
A lot a different topics are covered :
- standard scientific visualization (1D and 2D plots, points clouds, etc…)
- ODE solvers
- Dense and Sparse Linear Algebra solvers
- ML algorithms (Kmeans, PCA, etc…)
- FEM solvers
- Quadtree and Delauney Meshing
- Semi discrete Optimal Transport
- Symbolic Differentiation -> Geodesic equation solver (used for raytracing around black holes)
- Discrete Differential Geometry (Heat Geodesic Method, curvatures…)
- etc…





Simple raytracer/sphere-tracer
- raytracing for mesh and bezier surfaces
- sphere tracing for SDF modeling
- basic procedural generation



Fluid, Solid & Cloth interaction simulation
- Shallow water model for the fluid
- Mass Spring System for the cloth
- Rigid body dynamics for the boat
- (Shitty) Custom 3D rasterization engine for rendering
Misc :
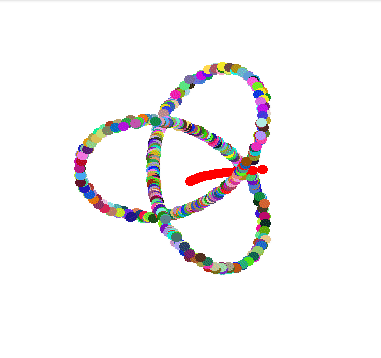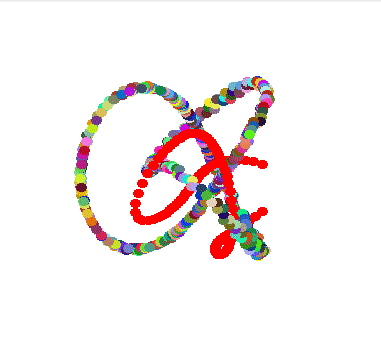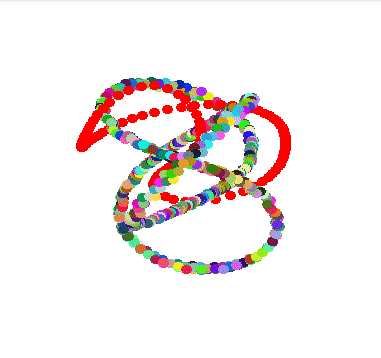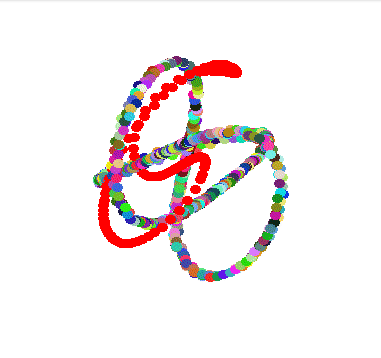
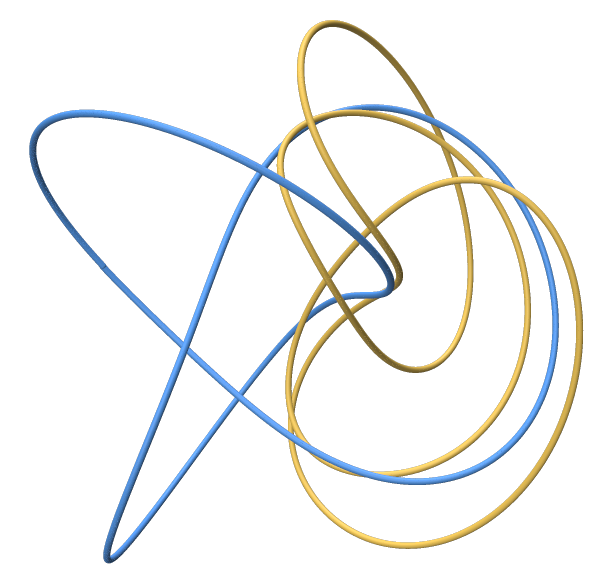
Modular knots, inspired by the amazing article of Etienne Ghys & Jos Leys. I will probably write a blog post or do a video about it because it was an amazing 4 year long journey where I often came back to improve the computations gradually.

